Union-Find

크루스칼을 알기 위해서는 Union-Find를 먼저 알아야합니다.

Disjoint Set

• 서로소 집합

Union-Find

• 서로소 집합을 표현할 때 쓰는 알고리즘.
• 다양한 자료구조를 통해 만들 수 있으나 트리구조가 가장 효율적이다.

Union-Find의 연산

1. make-set(x) : x를 유일한 원소로 하는 새로운 집합을 만든다. [x] <- 이런 식
2. union(x,y) : x가 속한 집합 + y가 속한 집합.
3. find(x) : x가 속한 집합의 루트 노드값(대표값)을 반환한다. 루트 노드는 x가 어떤 집합에 속해있는 지를 대표할 수 있다.

Union-Find의 과정

1. 초기화
   • P[i] = i인 상황.
   • P = [1,2,3,4,5]
2. union(1,2)
   • find(1)=1, find(2)=2 => p[2] = 1 (임의로 2를 1로 넣어줌. 둘 중 어떤 값을 해줘도 상관없음. 다만 일관성을 위해 작은 값을 무조건 대표값으로 하기로 하자.)
   • P = [1,1,3,4,5]
3. union(4,5)
   • find(4)=4, find(5)=5 => p[5]=4
   • P = [1,1,3,4,4]
4. union(1,4)
   • find(1)=1, find(4)=4 => p[4]=1
   • P = [1,1,3,1,4]

이런 식으로 계속 union을 해주고, union에서 루트노드를 찾기 위한 방법으로 find를 사용하게 된다.

위를 보면 결국 한 집합에는 겹치는 애들이 없게 된다.

• 인덱스 1을 대표로 갖는 값들 집합 : 1,2,4

• 인덱스 3을 대표로 갖는 값들 집합 : 3

• 인덱스 4를 대표로 갖는 값들 집합 : 5

이런 식으로 각 집합을 모두 더하면 결국 {1,2,3,4,5}가 되고 각 집합 간에는 중복되는 노드가 없다. 즉 서로가 상호배타적인 집합이다.

기본 구현

p = []
for i in range(N+1) :
    p.append(i)

def find(u) :
    if u != p[u] :
        p[u] = find(p[u]) # 경로 압축
    return p[u]

def union(u, v) :
    root1 = find(u)
    root2 = find(v)
    p[root2] = root1

최적화

트리가 완전 비대칭인 경우에는 말단 노드에서부터 루트 노드까지 N개의 노드를 전부 거치면서 가야한다. find는 O(N)이 되고, 이에 따라 union도 O(N)이 된다.

최적화가 안된 방식으로 find를 작성하면?

def find(u) :
    if p[u] == u : return u # 부모 노드는 자신의 노드 번호를 갖고 있으므로
    else :
        return find(p[u]) # 하나하나 찾아서 올라간다.

위의 형태가 된다. 그렇다면 경로 압축이 된 형태 부분을 주석과 함께 살펴보면 다음과 같다.

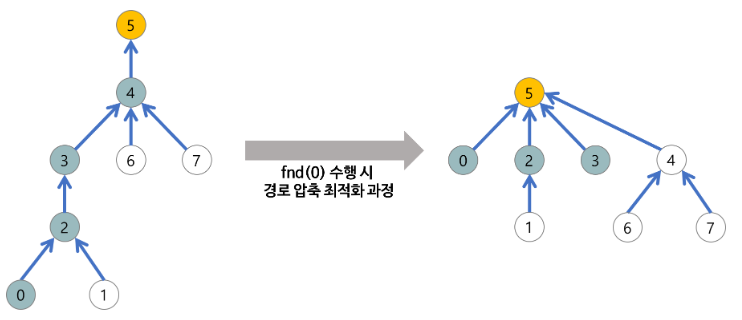
def find(u) :
    if u != p[u] : # 부모 노드가 아니라면
        p[u] = find(p[u]) # 부모 노드를 찾아서 업데이트 해준다.
    return p[u] # 부모 노드를 반환한다.

결국 find를 시행할 때, 이왕 하나하나 찾아서 올라가고 있으니까 그 부모노드 값으로 아예 업데이트를 해주어서 경로를 압축해버리는 것이다.

크루스칼Kruskal

프로그래머스의 섬 연결하기가 크루스칼 알고리즘을 활용해야 하는 문제입니다.

언제 쓰나요?

• 최소신장트리(MST; 무방향 가중치 그래프에서 간선의 가중치 합이 최소인 것)을 찾는 알고리즘입니다.

1. 사이클을 이루지 않는
2. 최소 비용 간선 집합을 구하고 싶을 때.

어떻게 쓰나요?

모든 선택에 있어 가중치가 최소인 선택을 하되, 사이클을 만들지 않는 노드를 선택합니다. (그렇기 때문에 섬 연결하기 문제가 그리디 문제로 분류되어 있습니다.)

1. 그래프의 간선들을 가중치의 오름차순으로 정렬
2. 사이클을 형성하지 않는 간선을 선택
   • 사이클 형성 여부 판별 : union-find를 사용하여, 해당 간선을 선택하면 사이클이 생기는지 판별합니다. 가령 n1, n2를 선택하려 할 때, n1의 부모 노드 == n2의 부모 노드 라면 사이클이 생기게 되겠죠?
   • 가장 가중치가 작은 간선을 먼저 뽑아내기 위해 heapq를 사용합니다.
3. 해당 간선을 MST 집합에 추가합니다.

정당성 증명

일반적인 그리디와 같은 형태로 최소신장트리임을 증명할 수 있습니다.

• 그리디 알고리즘의 증명
  1. greedy choice property : 탐욕적인 선택으로 인해 최소한 손해를 보진 않는다.
  2. optimal substructure : 항상 최적의 선택만을 내려도 전체 문제의 최적해를 얻을 수 있다.

신장트리 증명

• union-find를 통해 루트 노드가 겹치지 않는 노드만을 선택했으므로 신장트리임은 자명하다.

greedy choice property 증명

References

Union-Find